
Inspiration is needed in geometry,
just as much as in poetry.
– Alexander Pushkin
Introduction
”No one will embrace the immense!” Kozma Prutkov’s winged saying can be fully applied to the infinitely delightful geometry of triangles. With deep admiration and love for the discipline, we are presenting our creative article in synthetic geometry about configuration around incentre-midpoint line \( IM \), where we found a plethora of beautiful and surprising geometric properties. It consists of lemmas exploring the IM line configuration, some are not directly used in the solution, and an elegant finish to the main problem. Preliminary knowledge in Projective and Synthetic Geometry is recommended.
Problem Statement
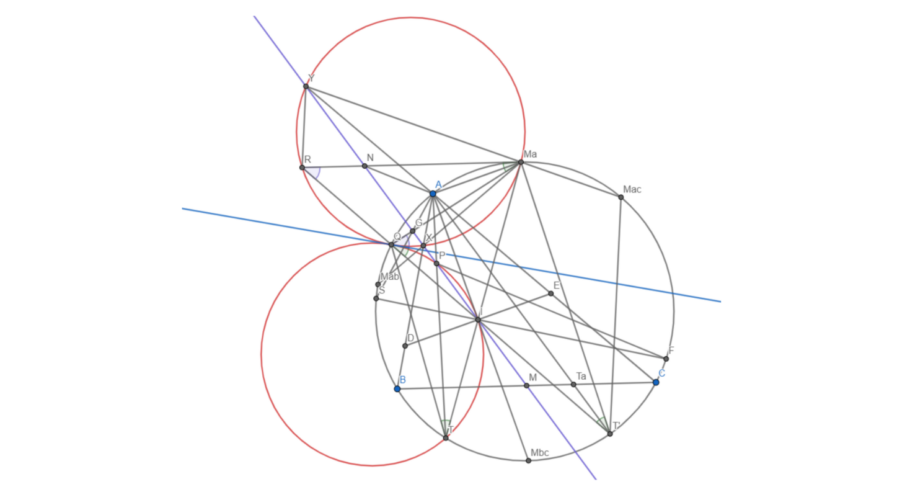
Given a scalene triangle \( ABC \), \( I \) — its incenter, \( M \) — midpoint of \( BC \), \( \omega \) — circumcircle of triangle \( ABC \), \( M_a \) — midpoint of arc \( BAC \) containing \( A \). Line \( M_aI \) intersects circumcircle at point \( T \). Line \( IM \) intersects lines \( AB \), \( AC \), and \( AT \) at points \( X \), \( Y \), and \( P \) respectively.
Prove that circumcircles of triangles \( TIP \) and \( M_aXY \) are tangent to each other.

Figure 1: Prove that blue circles are tangent.
Lemma 1: \( AT \) is tangent to circumcircle of \( (AXY) \).
Proof. Notice that \( T \) is a touching point of \( A \)-mixtilinear incircle with \( \omega \). By other well known properties of that point, \( AT \) and \( AT_a \) are isogonal with respect to \( \angle ABC \), where \( T_a \) is an extouch point of side \( BC \). And we also have that \( AT_a \parallel IM \), with that we can say that \( AT \) is tangent and moreover that \( \triangle TBC \sim \triangle AXY \).
Lemma 2: Line \( M_aX \) intersects arc \( \widehat{AC} \) of \( \omega \) in its midpoint — \( M_{ac} \).
Proof. If \( M_{bc} \) is arc \( AC \)’s midpoint, then Pascal’s theorem for \( CBM_{ac}M_aM_{bc}A \) yields the desired concurrency. Analogously we can show that \( M_aY \) intersects arc \( AB \) in its midpoint — \( M_{ab} \).
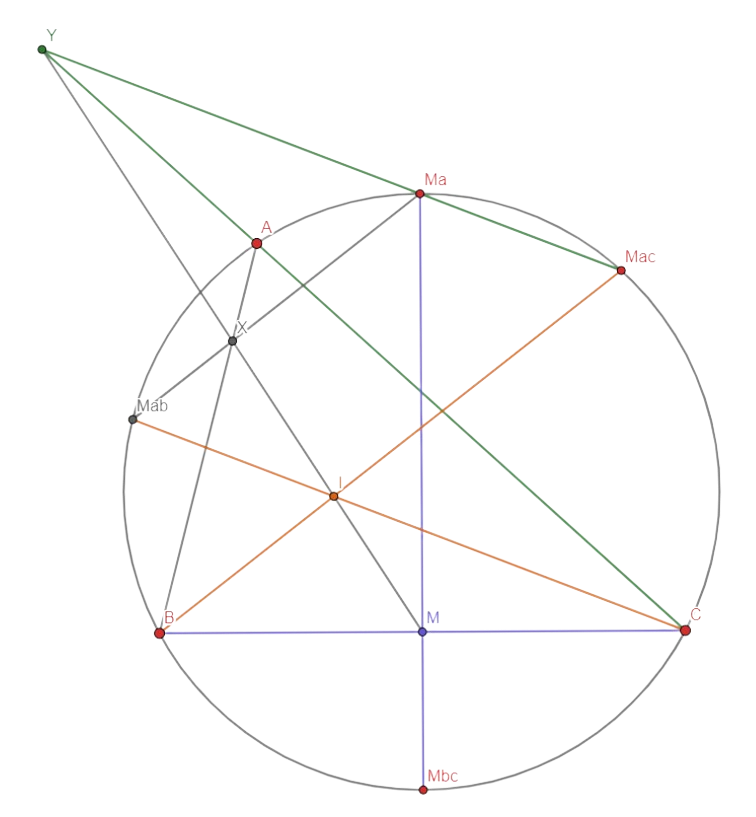
Figure 2: Pascal Theorem applied on the hexagon \( CBM_{ac}M_aM_{bc}A \).
Proof. \( \frac{BS}{SC} = \frac{BD}{EC} \) by similarity of \( BDS \) and \( CES \). Apply the bisector property WRT \( TD \) and \( TE \) (which are bisectors due to Lemma of Archimedes): \( \frac{BT}{BD} = \frac{AT}{DA} = \frac{AT}{EA} = \frac{TC}{EC} \) So \( \frac{BS}{SC} = \frac{BT}{TC} \) therefore \( BTCS \) harmonic.
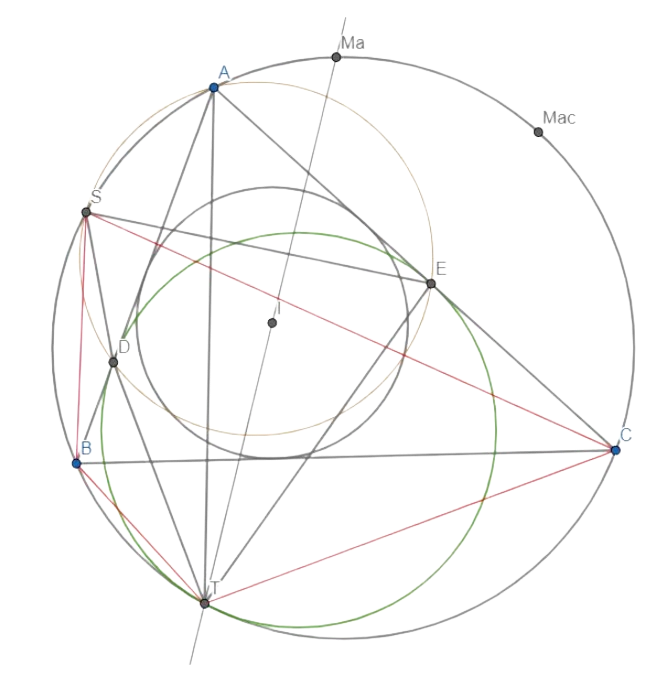
Figure 3: \( BTCS \) form a Harmonic quadrilateral in red.
Lemma 4: \( SXAY \) \(\sim \) \( SBTC \)
Proof. \( S \) is Miquel point of quadrilateral \( DBCE \) (by construction), so it is the center of spiral similarity that takes segment \( DE \) to segment \( BC \), and since \( I \) and \( M \) are their midpoints, it takes \( I \) to \( M \). By spiral similarity properties, we have that there is a spiral sim centered in point \( S \), that takes \( IM \) to \( EC \), so the Miquel point of quadrilateral \( IMCE \) is actually \( S \). So \( AXSY \) is inscribed. Next, we say that, by spiral similarity, \( SXY \sim SBC \) and we’ve already proved that \( TBC \sim AXY \), so we can conclude that \( SXY \sim SBTC \).
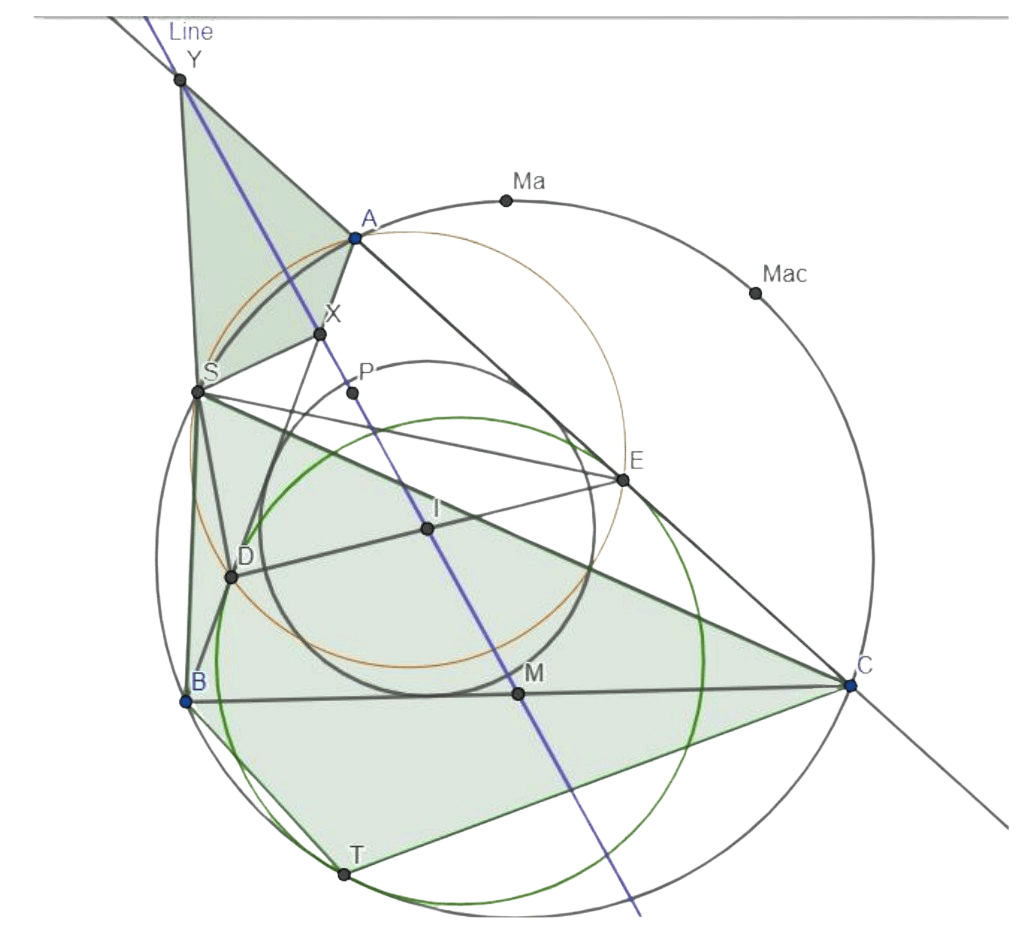
Figure 4: Similar quadrilaterals \( SXAY \) and \( SBTC \) are in green.
Lemma 5: \( P \) is the circumcenter of triangle \( SIA \). Therefore \( M_{ac}, M_{ab} \) and \( P \) are collinear.
Proof. Since \( \angle PAI = \angle IAT_a = \angle PIA, PI = PA \). Since there is a spiral similarity that takes \( DE \) to \( BC \), it also takes \( A \) to \( M_a \) (as centers of respective arcs) and \( I \) to \( M \) (as midpoints), so triangles \( SAI \sim SM_aM \), so \( \angle ASI = \angle M_aSM \). Now \( \angle CSM = \angle TSB \) (Because it’s a harmonic quadrilateral) = \( \angle TAB \), so \( \angle M_aSM = \angle M_aSC + \angle CSM = \angle TAB + \angle EDA = 90^\circ — \angle PAI \), so \( P \) is actually the circumcenter. Additionally, we get that \( M_{ac}M_{ab} \) passes through \( P \) since it is a perpendicular bisector of the line \( AI \) (by definition of circumcircle).
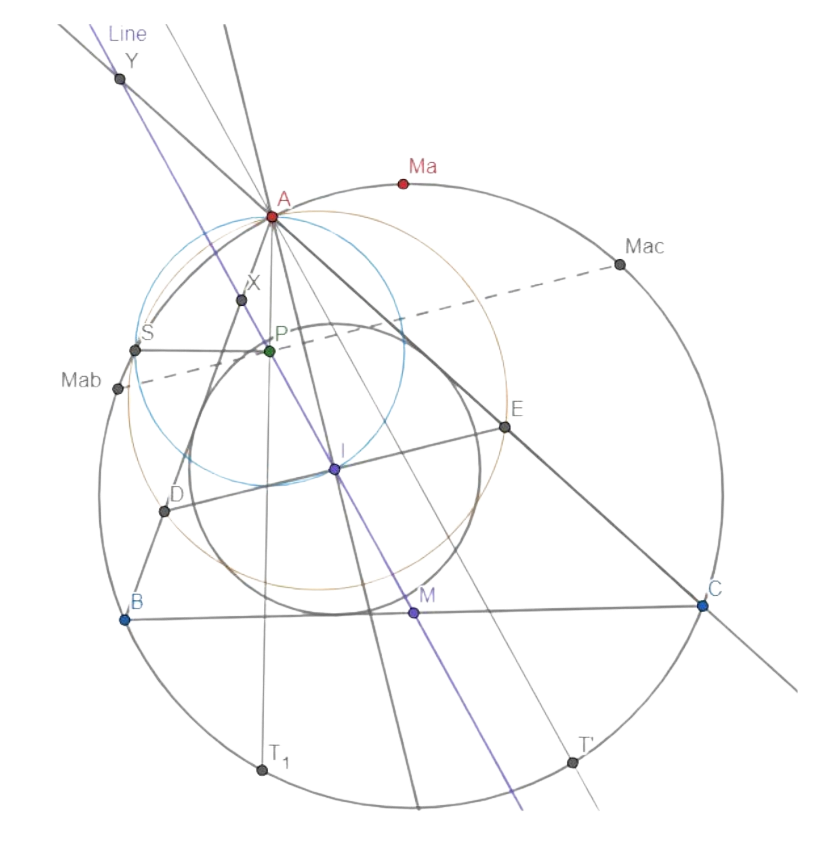
Figure 5: P is the circumcenter of the blue circle \( ASI \).
Lemma 6: Tangent to \( \omega \) at point \( M_a \) intersects \( XY \) at its midpoint.
Proof. Firstly, let’s prove that \( M_aI \) is tangent to \( (M_aXY) \). Angle chasing: \( \angle XYY_{M_a} = \angle(M_{bc}M_a, AT_a) = \angle TA_{AC} + \angle CAM_{ac} — \angle ACM_{a} = \angle TA_{AC} + \angle M_{ab}AB = \angle IM_aX \), which is what we had to show. Now, Suppose that the point of intersection is \( N \). Let \( T’ = AT_a \cap \omega \) and \( F’ \) be a point on \( \omega \), so that \( M_aF \parallel IM \parallel AT’ \). Now \( M_{aF} = M_{aT’} — FT’ = M_{aT} — M_{aA} = AT’ \), that completes the proof.