Введение

Одним из главных достижений Физики 19-го века считается Распределение Максвелла (нынешне его сливают вместо с понятием Распределение Больцмана, порождая Распределение Максвелла-Больцмана). Оно помогает нам рассматривать движения огромного числа частиц, отвлекаясь от индивидуального движения самих частиц. Данное распределение есть закон статистический, то есть оно применимо лишь к большим наборам частиц. Рассмотрев газ из пары молекул, оно уже работать не будет, поэтому важно понимать при каких случаях его стоить применять. Для наглядности, покажем на примере давления:

Рассмотрим молекулу, что находится в замкнутом сосуде. Она будет время от времени соударяться со стенками сосуда, что будет выражено в качестве какой-то сил, действующей на стенки в течение короткого промежутка времени. Такие удары будут хаотичны и дискретны, никакого среднего давления здесь не будет. Увеличив число частиц, мы будем выглаживать график оказываемой силы, и поэтому давления. При колоссальном числе частиц, мы получим картинку, где есть средняя величина давления с чрезвычайно малыми флюктуациями от этого значения. Точно так же, это рассуждение может быть применено и к Распределение Максвелла.

Цель данной статьи, вместо того, чтобы описывать уже описанные в учебниках средней и старшей школы по Физике темы, я предлагаю рассмотреть как мы можем использовать данное распределение в необычном 2D случае бильярдного стола с огромным количеством маленьких шаров на нем.

Формулировка Проблемы

Здесь показана область, где координата x заключена в интервале  (0.4 — 0.01, 0.4 +0.01). Площадь, что находится под кривой и в данном интервале, даст вероятность нахождения координаты в этом самом интервале. 

На данном графике представлены частицы, чье значение скорости равно 3 м/с

В таком пространстве скоростей удобно представить вероятность того, что скорость частицы будет найдена в объеме $dv = dv_x \, dv_y \, dv_z$:

(3) $dP = f_x \times f_y \times f_z \times dV$

Здесь функции распределения взяты в направлении соответствующих осей.

Решение

Разобравшись в основных идеях, перейдем к решению самой задачи. Поскольку это двухмерный случай, здесь представлены две функции распределения:

(4) $f_y(v_y) = \sqrt{\frac{m}{2\pi kT}} \exp\left(-\frac{mv_y^2}{2kT}\right)$

(5) $f_x(v_x) = \sqrt{\frac{m}{2\pi kT}} \exp\left(-\frac{mv_x^2}{2kT}\right)$

Здесь N  есть количество шаров на столе. Найдем, смысл этого я поясню позже, количество шаров, что движутся с определенной скоростью $v$, без учета их направления:

На данном графике представлены частицы, чье значение скорости заключено от 2 м/с до 2.2 м/с 

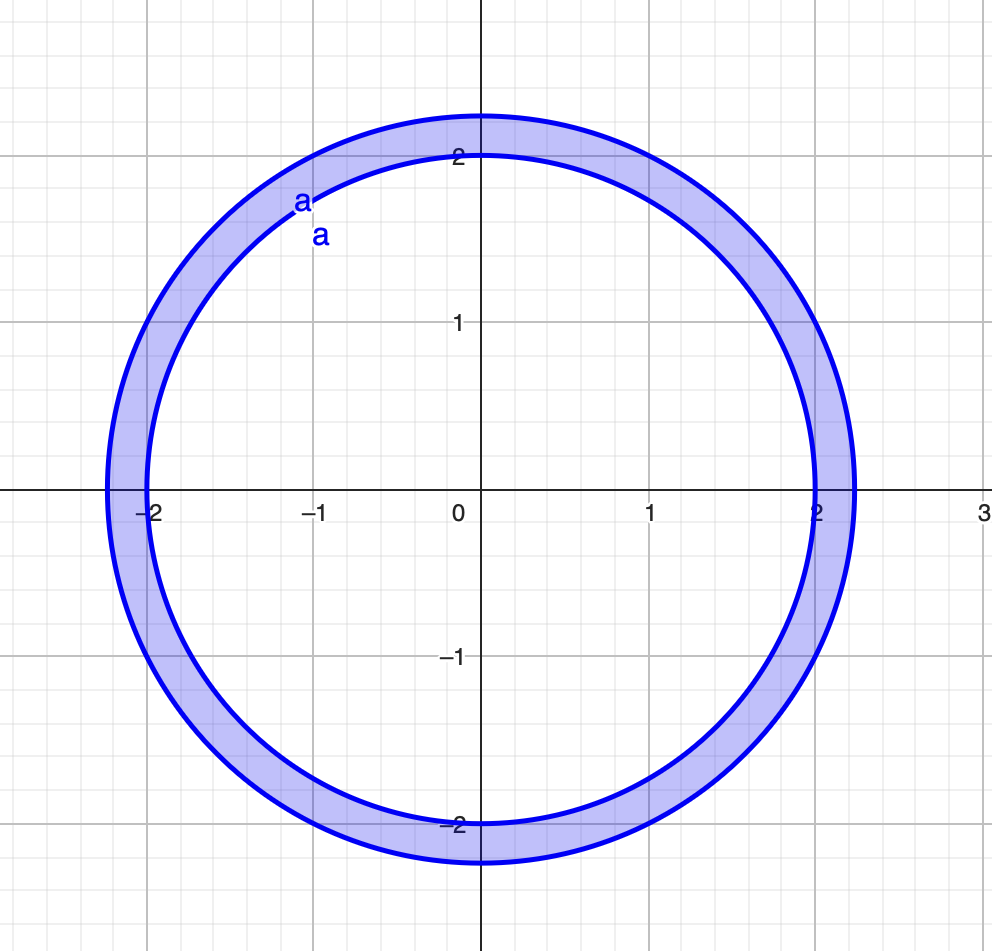
Рассмотрим шары, чья скорость разбросана в пределах ($v$, $v$+$dv$). Вероятность их нахождения в этом пределе есть:

(7) $dP_1 = f_x \times f_y \times dV$

(8) $dV$ = $2\pi v \, dv$

Тогда их концентрация есть произведение $n$ и $dP$. Теперь, рассмотрим сколько таких частиц движутся под углами ($\alpha $, $\alpha +d\alpha$) к нормали к лунке:

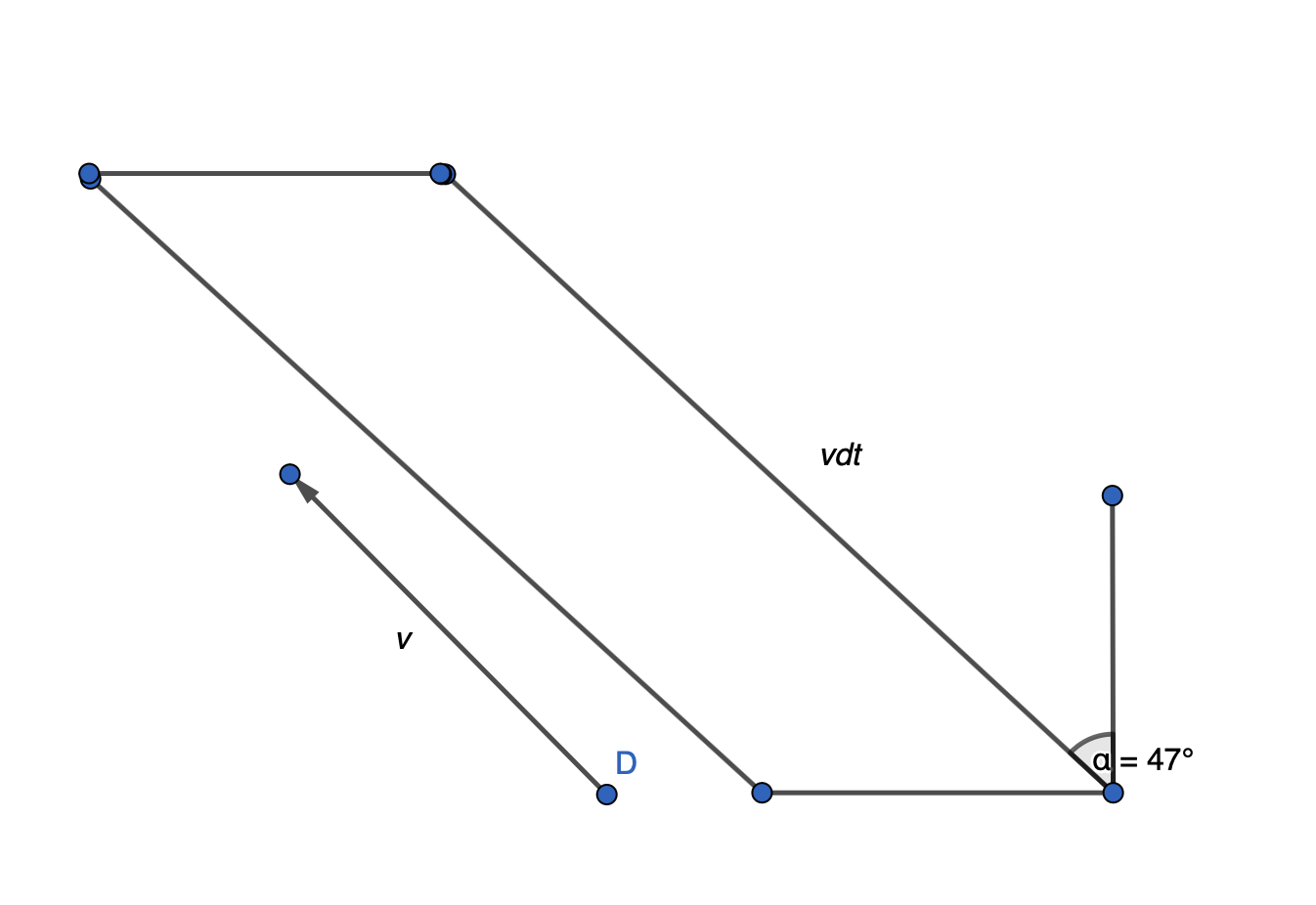
Вероятность, того что шары движутся в этом пределе, есть:

(9) $dP_2$ = ${d\alpha}/{2\pi}$

Тогда вероятность того, что частица движется со скоростями ($v$, $v$+$dv$) и углами ($\alpha $, $\alpha +d\alpha$), есть произведение $dP_1$ и $dP_2$.

За малое время $dt$ данные шары они пройдут путь $vdt$. Тогда, предполагая что основание есть длина лунки $l$, они заметут площадь $vdtcos\alpha l$. Их количество есть:

(10) $dN$ = $n\times dP_1\times dP_2\times vdtcos\alpha l$

Тогда количество, на которое уменьшается число шаров на столе, дастся формулой:

(11) $dN_{(\alpha,v)} = -\frac{Nmv^2 l \cos(\alpha)}{2\pi kTS} e^{-\frac{mv^2}{2kT}} d\alpha dvdt$

Тогда, проинтегрировав данное выражение по углу от $-\pi / 2$ до $\pi / 2$ и по скоростям (0, +$\infty$), получим:

(12) $dN/dt = — \sqrt{\frac{kT}{2m\pi}}Nl/S$

Мы получили расход частиц по времени, что зависит от количества частиц и… температуры? Что есть температура бильярдных шаров? Из МКТ газов мы знаем, что температура характеризует среднюю энергию частиц газа. В случае атомов, она дается:

(13) $E$ = $3kT/2$, где 3 появляется, так как атомы движутся в трех измерениях без вращений

Тогда, мы можем аналогично расписать температуру бильярдных шаров:

(14) $E$ = $2kT/2$ = $kT$

(Теперь может стать понятно почему температуру Солнца часто измеряют в единицах энергии, электронвольт)

Теперь, выяснив смысл T и выразив среднюю энергию, мы можем записать энергию как $mvˆ2/2$? Тоже неверно, потому что средняя энергия выражается через среднюю квадратичную скорость, а нам дана средняя скорость. Чтобы найти связь между средней скорость и средней энергией, применим стандартную формулу:

(15) $\bar{x} = \int xf(x)dx$, где интеграл берется по нужному интервалу, $f(x)$ есть плотность вероятности и x есть некая переменная. В случае средней скорости:

(16) $\bar{v} = \int_{0}^{\infty} v2\pi v \frac{m}{2\pi kT} \exp\left(-\frac{mv^2}{2kT}\right)dv$

(17) $\bar{v} = \sqrt{\frac{\pi kT}{8m}}$

Для средней энергии:

(18) $\bar{E} = \int_{0}^{\infty} E2\pi v \frac{m}{2\pi kT} \exp\left(-\frac{mv^2}{2kT}\right)dv$

(19) $\bar{E} = \frac{1}{kT}\times \int_{0}^{\infty} E \exp\left(-\frac{E}{kT}\right)dE$

(20) $\bar{E} = kT$ ( мы просто доказали формулу 14, которую можно было получить и используя теорему о равнораспределение энергии по степеням свободы )

Теперь мы можем просто выразить температуру и подставить среднюю скорость в формулу (12) и проинтегрировать? Тоже нет. Данный подход был бы верен, если бы температура, а с ней средняя энергия шаров, не изменялась бы, а это не так. Более быстрые частицы имеют больше шансов покинуть стол, а значит в среднем остается больше медленных шаров, вызывая уменьшение средней энергии. Чтобы найти какую энергию уносят шары в среднем, вернемся к формуле (11). Она дает количество шаров, что движутся со скоростями ($v$, $v+dv$) и значит они уносят в среднем энергию:

(21) $dEtotal= -E\times \frac{Nmv^2 l}{\pi kTS} e^{-\frac{mv^2}{2kT}}dvdt$

Тогда, упростив выражение, получим:

(22) $dEtotal = -kT\times \frac{Nl}{\pi S}\times \sqrt{\frac{\pi kT}{8m}}$

Теперь, взяв интеграл по энергии от нуля до $\infty$, найдем:

(23) $dE/dT = — 3kT\times Nl/\pi S \times \sqrt{\frac{\pi kT}{8m}}$

E это полная энергия шаров на столе, поэтому:

(24) $E$ = NkT

Подставив это в (23):

(25) $dN/dt\times T + dT/dt\times N = — 3T\times Nl/\pi S \times \sqrt{\frac{\pi kT}{8m}}$

Теперь, решая вместе (25) и (12), мы получим систему дифференциальных уравнений. Подставим (12) в (25), тогда получим:

(26)$\sqrt{\frac{kT}{2m\pi}}lT/S + dT/dt = -3/2\sqrt{\frac{kT}{2m\pi}}lT/S$

Чтобы упростить выражение, заменим $\sqrt{\frac{k}{2m\pi}}l/S$ константой C:

(27) $dT/dt = — 5/2\times C\times T^{\frac{3}{2}}$

(28) $\int_{T_0}^{T}T^{-\frac{3}{2}} dT = -5/2Ct$

(29) $1/\sqrt{T} — 1/\sqrt{T_0} = 5/4Ct$

(30) $\sqrt{T} = \frac{4\sqrt{T_0}}{5C\sqrt{T_0}t +4}$

Найдя как меняется температура от времени, подставим (30) в (12):

(31) $dN/dt = -\frac{4C\sqrt{T_0}}{5C\sqrt{T_0}t+4}\times N$

(32) $dN/N = — \frac{4C\sqrt{T_0}}{5C\sqrt{T_0}t+4}\times dt$

Проинтегрировав (32) слева от $N_0$ до $N_0/2$ и справа от нуля до $t$, получим:

(33) $1/2 = (\frac{5C\sqrt{T_0}t+4}{4})^{-\frac{4}{5}}$

Выразив теперь $T_0$ через начальную среднюю скорость, используя (17):

(34) $\sqrt{T_0} = \sqrt{\frac{8m}{\pi k}}\times v$

(35) $C\sqrt{T_0} = \frac{2vl}{\pi S}$

Тогда (33) перейдет в:

(36) $1/2 = (\frac{\frac{10vlt}{\pi S}+4}{4})^{-\frac{4}{5}}$

(37) $2^{\frac{5}{4}} — 1 = 5/2\times \frac{vlt}{\pi S}$

Отсюда время, за которое число шаров упадет вдвое, выражается как:

(38) $t = \frac{2\pi S (2^{\frac{5}{4}}-1)}{5vl}$

Таким вот образом решается данная задача. Наличие площади в числителе логично, ведь чем больше стол, тем больше времени понадобится шарам, чтобы добраться до лунки. Так же, чем больше скорость и длина лунки, то тем быстрее шары будут вылетать со стола, уменьшив время. Для окончательного завершения, распишем длину лунки $l$ как $2R$:

(39) $t = \frac{2\pi S (2^{\frac{5}{4}}-1)}{10vR}$