Предисловие

Эта статья будет посвящена использованию инженерного калькулятора на физических олимпиадах. Сам еще будучи только вступая на путь олимпиадной физики мне пришлось столкнуться с проблемой: А как правильно использовать инженерный калькулятор?  Статья рассчитана на тех, кто умеет пользоваться обычными функциями и инструментами в калькуляторе и хочет раскрыть потенциал своего «помощника» еще шире.

Работать мы будем с калькулятором CASIO fx-991 EX CLASSWIZ. Т.к. я сам им пользуюсь и рекомендую именно его.

Переменные

А начнем мы с переменных!

Разберемся с начала для чего они нужны и как они упрощают нашу жизнь.

Рассмотрим пример:

Вам нужно провести большое число расчетов, в которых фигурируют несколько констант. Бывают случаи, когда эти несколько констант можно заменить одной. Что делает обычный пользователь калькулятора? Он либо смиряется с этим (это точно не наш случай, пока вы будете в каждой формуле отдельно писать численные значения этих констант утечёт драгоценное время) или же где-нибудь на черновике записывает их приближенное значение (значение конечно же не всегда получается «красивым») и потом использует его в своих расчётах. У такого подхода есть два существенных недостатка:

1) Из-за приближений есть возможность получить «достаточные» погрешности чтобы вам сняли пару баллов

2) Вы можете ошибиться в какой-нибудь цифре, и тогда будет очень неприятно узнать, что вы потеряли медаль из-за банальной вычислительной ошибки

Чтобы избежать таких казусов и придуманы переменные. Они позволяют один раз занести число в память калькулятора с помощью какого-то символа (например, английской буквы A или x) и потом использовать его в дальнейших расчетах, иногда очень громоздких(но что поделать, такова жизнь физика).

Перейдем к практике:

Для использования переменных на калькуляторе вам всего нужны будут две функции:

STO

RECALL (данная функция вызывается последовательным нажатием кнопки SHIFT и STO)

Как ими пользоваться и что они означают?

Начнем с STO. Эта функция отвечает за запоминание вашего числа в конкретной ячейке. Эта ячейки памяти обозначаются английскими буквами: A, B, C, D, E, F, M, x и y. В них хранится ваше число. Приведем пример: Вы «положили» число, скажем 5763,345 в ячейку под буквой А. Т.е. теперь вместо того, чтобы писать 5763,345 вы можете написать просто букву А, и калькулятор при вычислении будет считать А соответствующим числом (в нашем случае числом 5763,345). Для того чтобы набрать букву А вы должны сначала нажать на кнопку ALPHA и потом на (-). Как не сложно догадаться, чтобы пользоваться желтыми функциями вы должны сначала нажать кнопку SHIFT и потом кнопку с функцией, над которой написана нужная вам функция. Аналогично следует поступать и с красными функциями (здесь вместо SHIFT нужно нажать сначала ALPHA).

Запоминание числа в ячейке происходит следующим образом:

• Вам нужно ввести число (например, 5763,345)
• Нажать кнопку STO
• Нажать кнопку c названием ячейки, в которую вы хотите сохранить это число (НО, здесь вам НЕ нужно нажимать ALPHA)

Теперь вы можете продолжать ваши расчёты.

(Чтобы обнулить содержимое ячейки, нужно проделать те же действия, но только вместо условного числа 5763,345 вы должны написать 0)

Иногда бывают ситуации, когда вы использовали большое число переменных и попросту забыли какие у них значения и за что они отвечают. Функция RECALL позволяет вам просмотреть ВСЕ значения ваших переменных. (Чтобы её вызвать нажмите комбинацию SHIFT и STO).

Продолжаем наше познание калькулятора, на очереди метод линеаризации.

Линеаризация и МНК

Рассмотрим, как линеаризировать зависимость на конкретном примере:
Допустим у вас есть нелинейная зависимость y=5x^2+4,9. Ваша задача сделать так чтобы эта зависимость стала линейной. В данном случае это можно сделать заменяя x^2 на другую переменную, пусть будет z. Тогда у нас получается линейная зависимость y=5z+4,9. Таблица значений для данного случая будет выглядеть вот так:

Прочитать более подробно о методах и способах линеаризации и использовании Метода Наименьших Квадратов (МНК) вы можете в книге замечательного автора А.И. Слободянюка «Физическая олимпиада: экспериментальный тур»
, а мы рассмотрим, как эти методы осуществляются в калькуляторе.

 

Для обработки линейных зависимостей вам нужно в первую очередь перейти в 6 раздел (Statistics): Нажмите Menu и выберите соответствующий раздел.

Перед вами открывается большое число видов уравнений (а точнее 7: со 2 по 4 и с 1 по 4 на следующей «странице»). Мы будем с вами пользоваться только одним: y= a+bx. Нажмите цифру два, чтобы открыть его.

Рассмотрим такой пример:

Вы получили какие-то значения какой-то зависимости и хотите проверить линейная она или нет. Для этого внесите ваши иксы и соответствующие им игреки в калькулятор. Далее нажмите кнопку OPTN и выберите раздел под номером 4 (Regression Calc).

У вас должно быть так:

Калькулятор показывает саму линейную функцию (обратите внимание что a – это СВОБОДНЫЙ член, а b – это член ПЕРЕД ИКСОМ так называемый угловой коэффициент), значения a и b, и значение коэффициента корреляции r. Как раз коэфф. корреляции и показывает схожесть вашей эмпирической формулы с линейной зависимостью (Чем он ближе к 1 или к -1, тем ваша зависимость более приближена к линейной).

С помощью таких манипуляций можно установить линейна ли ваша зависимость и найти коэффициенты этой зависимости. Проверка на подобие к другим зависимостям квадратичной (3), логарифмической (4) и т.д. не доступна, т.к. калькулятор не считает коэффициент корреляции для этих зависимостей. Тут очень важно понимать, что я говорю про проверку «в лоб», конечно, вы можете (и вам придётся) линеаризировать данную зависимость (т.е. привести её к виду y=a+bx) и уже потом посмотреть на коэфф. корреляции и сделать соответствующие выводы.  Всё это можно сделать и с помощью формул МНК вручную, но это очень затратно по времени и надежность таких расчетов будет под сомнением (вдруг вы где-то забыли злополучный минус или не написали двойку). (Вернуться к вашим иксам и игрекам можно нажав кнопку AC).

Но главная досада любого физика заключается в том, что иногда требуется посчитать погрешности ваших расчётов по формулам МНК, а калькулятор не обладает такой функцией. Но он всё еще не бесполезен!

На ряду с определением a, b и r он еще вычисляет дисперсии, средние значения, количество введенных вами иксов (и соответственно игреков) и многое другое что очень хорошо упрощает жизнь в расчётах погрешностей (остаётся только подставить выданные калькулятором вам значения и произвести простейшие расчёты).

Чтобы их узнать, вам нужно выбрать OPTN и раздел под номером 3 (2-Variable Calc).

Метод Ньютона

Следующая функция которой стоит посветить несколько минут своей жизни это Метод Ньютона. Мало кто вообще о ней знает, но иногда она может дать вам несколько нелишних баллов на олимпиаде.

Сначала пару слов о самом методе Ньютона. Метод Ньютона позволяет нам находить решения довольно сложных нелинейных уравнений. Его суть заключается в том что задается начальное приближение вблизи предполагаемого корня данного уравнения, далее строится касательная к графику исследуемой функции в точке приближения и абсцисса точки пересечения этой касательной с осью абсцисс берётся в качестве следующего приближения(т.е. следующая точка приближения находиться на графике с ординатой соответствующей абсциссе точки пересечения).

Чтобы использовать метод Ньютона, вам сначала нужно написать уравнение.

Для примера возьмём уравнение десятой степени х^10+5x^8-9x+3=0. Калькулятор просто так решить его не может т.к. стоит ограничение на максимально возможную степень, которая равна 4 (см. раздел А: Equation/Func, Polynomial (2)). На помощь приходит метод Ньютона.

После написания уравнения нужно нажать кнопку SOLVE (SHIFT и CALC).

В выведенный вам х вы должны ввести наиболее близкое предполагаемое вами значение (или можно довериться калькулятору и ничего не менять). Я выберу число 10.

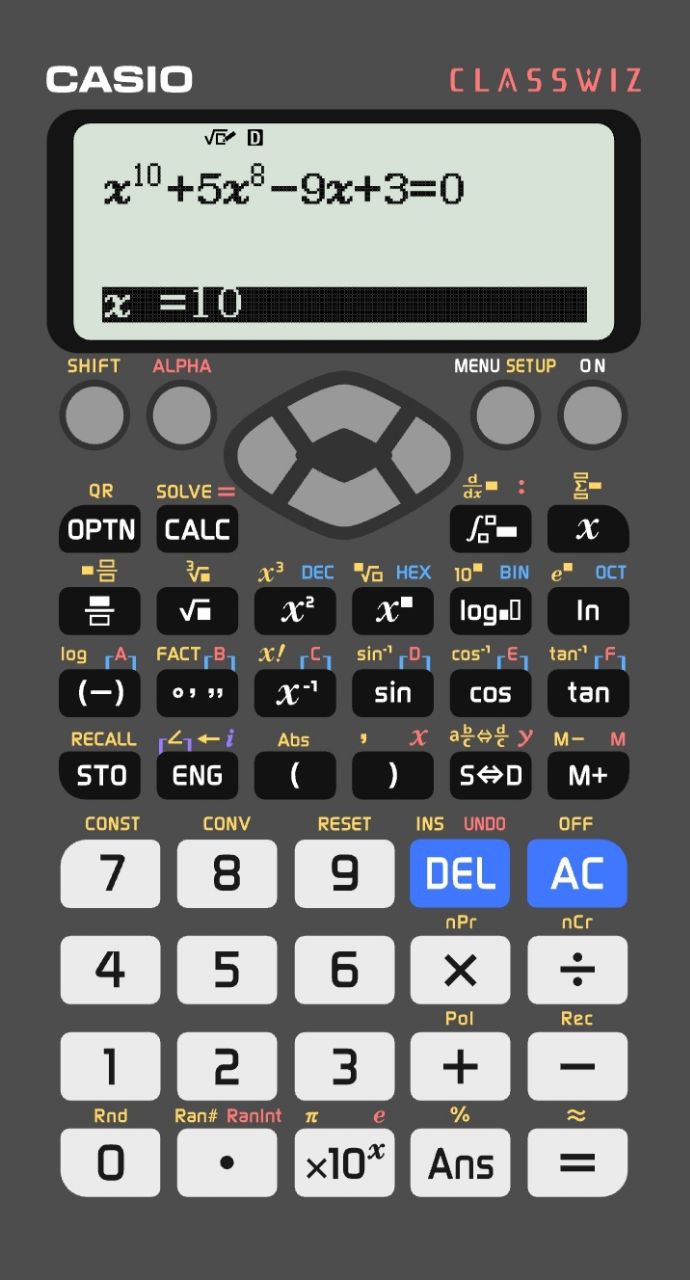
Нажимаем равно и дожидаемся подсчёта.

Ну вот и всё, вы получили один из корней данного уравнения:

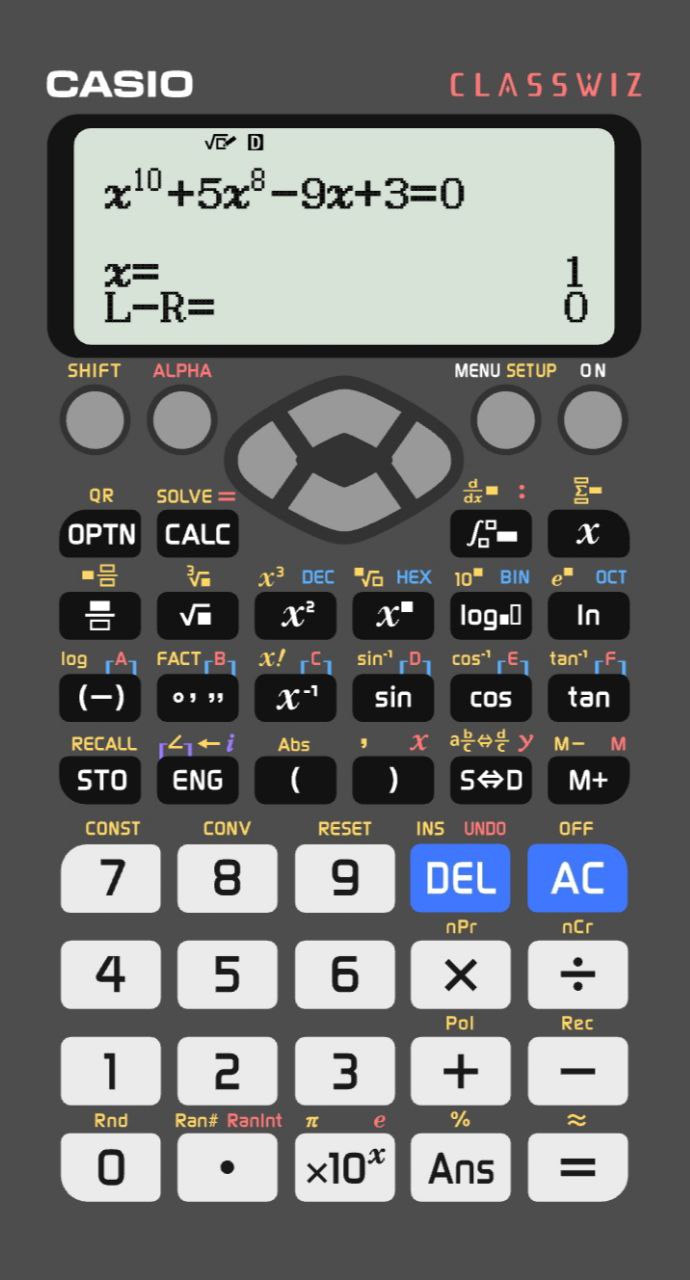
А что обозначает эта непонятная разность L-R?

Это так называемая разность (приближения слева) – (приближение справа), чем значение этой разности ближе к нулю, тем выше точность решения уравнения (у нас получился ноль, что говорит, что наш ответ точнее и быть не может). (Чтобы выйти из функции, нажмите клавишу AC).

Важные оговорки и замечания по методу Ньютона:

Если уравнение содержит функции со скобками (sin или log) нужно обязательно вводить закрывающую скобку.

Для функции SOLVE сходимость выполняется определенное количество раз. Если решение не будет найдено, то на дисплее отобразиться сообщение «Continue: [=]» (Продолжить: [=]). Нажмите равно для продолжения поиска решения или AC для отмены вычислений.

Функция SOLVE может не найти решение если будет введено начальное значение x (переменная для решения) далекая от истины. Попробуйте изменить начальное значение, на более приближенное к искомому решению.

Иногда бывает, что функция не может найти решение какого-то уравнения, даже если оно существует, но это случается довольно редко.

Следующий очень важный момент заключается в том, что метод Ньютона вам выдаст только одно решение, даже если их существует несколько.

(Чтобы данную проблему хоть как-то исправить советую всегда брать различные начальные значения х, отрицательные и положительные, большие и малые). Вернемся к нашему примеру и возьмём что начальное значение равно -10:

Мы получили еще один ответ (скажу по секрету, что в этом уравнении всего два не комплексных ответа, мы их и нашли)

Еще один недостаток метода Ньютона заключается в том, что из-за ограничений в самом методе, правильные решения трудно получить для уравнения вида: $y = \sin(x)$, $y = e^{x}$, $y = \sqrt{x}$
Бывает так что метод Ньютона выдает ответ с погрешностью (разность L и R не равна 0) и часто данная проблема решается с помощью использования в качестве начального значения уже полученный приближенный ответ. Для этого вам нужно два раза нажать равно и если повезет, то получите точный ответ (разность L-R будет равна нулю), иногда такую манипуляцию нужно проделать несколько раз (она занимает считанные секунды).

На этом изучение метода Ньютона можно закончить.

Заключение

Подводя итоги, хотелось бы сказать ещё раз о том, что все эти рассмотренные три раздела (переменные, МНК и метод Ньютона) чрезвычайно важны при решении физических задач, особенно практических. Они экономят ваше драгоценное время на олимпиаде и дают лучшую точность и надежность при поиске правильного ответа.