Задача №1

Условие

Вблизи точки $A$ (см. рис.) границы раздела стекло-вакуум напряженность электрического поля в вакууме $E_0$, угол между вектором $E_0$ и нормалью $n$ к границе раздела — $\alpha_0$. Необходимо найти напряженность $E$ поля в стекле вблизи точки $A$, угол $\alpha$ между векторами $E$ и $n$, а также поверхностную плотность связанных зарядов.

 

Решение

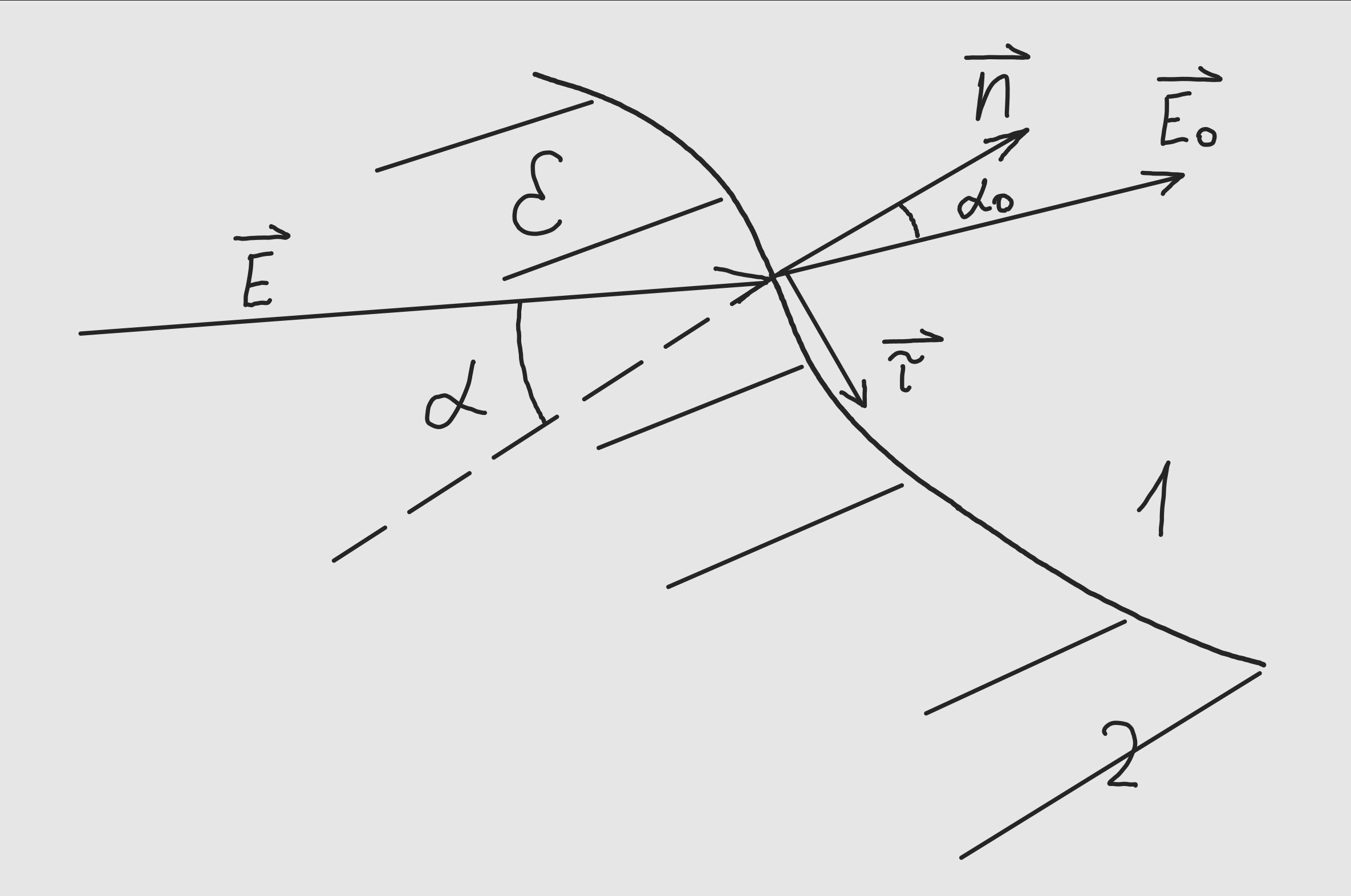
Рассмотрим граничные условия:

(1)  $ E_{1\tau} = E_{2\tau} $

$ D_{1n} — D_{2n} = 4\pi\sigma = 0 $ ⇒ $ D_{1n} = D_{2n} $ (2)

( $ \sigma = 0 $ т.к. нет свободных зарядов )

Расписываем их:

(1) $ E_0 \sin \alpha_0 = E \sin \alpha $

(2) $ E_{1n} = E_{2n} + 4\pi P_n = \varepsilon E_{2n} $

Тут использована формула $ \vec{D} = \vec{E} + 4\pi \vec{P} = \varepsilon \vec{E} $ , а также учтено, что $ P_{1n} = 0 $ (т.к. 1 среда-вакуум, а следовательно там нет поляризационных зарядов)

Из (2) следует, что:

$ E_0 \cos \alpha_0 = \varepsilon E \cos \alpha $  ⇒  $ E \cos \alpha = \frac{E_0 \cos \alpha_0}{\varepsilon} $ (3)

Наша цель избавится от α, поэтому выражаем $ E \cos \alpha $ и возводим его в квадрат складывая с квадратом $ E \sin \alpha $ :

$ E^2 \cos^2 \alpha + E^2 \sin^2 \alpha = \frac{E_0^2 \cos^2 \alpha_0}{\varepsilon^2} + E_0^2 \sin^2 \alpha_0 = E^2 $

$ E = \sqrt{\frac{E_0^2 \cos^2 \alpha_0}{\varepsilon^2} + E_0^2 \sin^2 \alpha_0} = \fbox{$\frac{E_0}{\varepsilon} \sqrt{\epsilon^2 \sin^2 \alpha_0 + \cos^2 \alpha_0} $} $

Находим угол:

Из (1) и (3):    $ \frac{E \sin \alpha}{E \cos \alpha} = \left( \frac{E_0 \sin \alpha_0}{E_0 \cos \alpha_0} \right) \varepsilon $ ⇒

⇒ $\fbox{$ \tan \alpha = \varepsilon \tan \alpha_0$} $

 

Далее нам нужно найти проекцию вектора поляризации $ \vec{P} $ на нормаль $ \vec{n} $ т.е. $ P_n $ :

Из (2)  $ P_n = (\varepsilon — 1) E_{2n} = \left| E_{2n} = \frac{E_{1n}}{\varepsilon} = \frac{E_0 \cos \alpha_0}{\varepsilon} \right| = (\varepsilon — 1) \frac{E_0 \cos \alpha_0}{\varepsilon} $

Используя равенство $ P_n = \sigma’ $ находим поверхностную плотность поляризационных зарядов:

$ \fbox{$\sigma’ = \frac{\varepsilon — 1}{\varepsilon} E_0 \cos \alpha_0$} $

 

 

Задача №2

Условие

Точечный сторонний заряд $q$ находится в центре диэлектрического шара радиуса $a$ с проницаемостью $\varepsilon_1$. Шар окружен безграничным диэлектриком с проницаемостью $\varepsilon_2$. Найти поверхностную плотность связанных зарядов на границе раздела этих диэлектриков.

 

 

 

Решение

Где формула (4) является так называемой теоремой Гаусса для вектора $D$.

Из формулы (3) видно, что поверхностная плотность связанного заряда определяется скачком поляризованности при $r = a$. То есть, чтобы решить нашу задачу, нужно найти проекции векторов поляризованности в двух средах на нормаль к поверхности шара.

Используя формулу (4) для двух поверхностей, получаем следующие результаты:

$D_1 \cdot 4 \pi r^2 = 4 \pi q \quad (\text{для поверхности внутри шара, вблизи границы } r = a)$
$D_2 \cdot 4 \pi r^2 = 4 \pi q \quad (\text{для поверхности снаружи шара, вблизи границы } r = a)$

Вычисляем напряженности полей и поляризованности:

$E_1 = \frac{D_1}{\varepsilon_1} = \frac{q}{\varepsilon_1 r^2}$
$E_2 = \frac{D_2}{\varepsilon_2} = \frac{q}{\varepsilon_2 r^2}$

$P_1 = \frac{D_1 — E_1}{4 \pi} = \frac{q}{4 \pi r^2} \left( 1 — \frac{1}{\varepsilon_1} \right)$
$P_2 = \frac{D_2 — E_2}{4 \pi} = \frac{q}{4 \pi r^2} \left( 1 — \frac{1}{\varepsilon_2} \right)$

Векторы $E$, $D$, $P$ сферически симметричны, то есть проекции этих векторов на нормаль будут модулями самих векторов.

Из третьей формулы вычисляем поверхностную плотность связанных зарядов:

$\sigma’ = \frac{q}{4 \pi a^2} \left( 1 — \frac{1}{\varepsilon_1} — 1 + \frac{1}{\varepsilon_2} \right) = \frac{q}{4 \pi a^2} \left( \frac{1}{\varepsilon_2} — \frac{1}{\varepsilon_1} \right) = \frac{q}{4 \pi a^2 \varepsilon_1 \varepsilon_2} \left( \varepsilon_1 — \varepsilon_2 \right)$

Таким образом, окончательное выражение для поверхностной плотности связанных зарядов:

$\boxed{\sigma’ = \frac{q}{4 \pi a^2 \varepsilon_1 \varepsilon_2} \left( \varepsilon_1 — \varepsilon_2 \right)}$

Источники