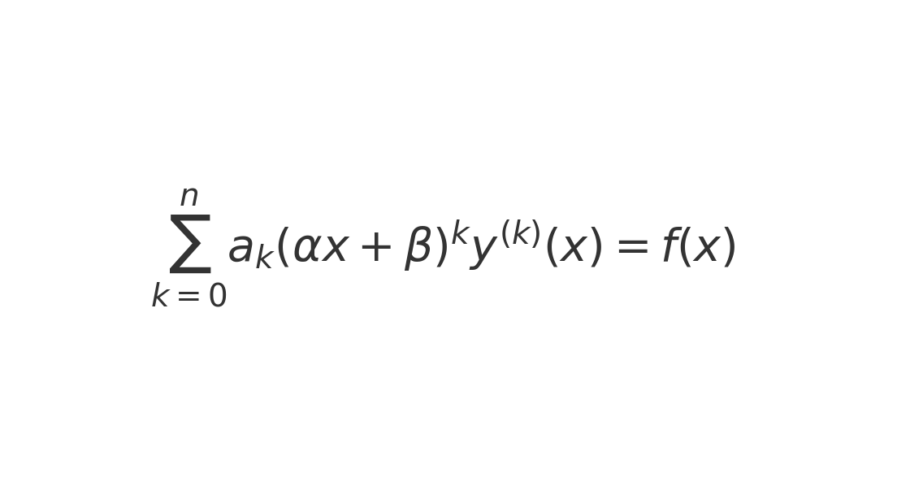{"markdown":"# I Introduction: What is Euler\\'s Equation?\r\n\r\n\u041c\u043d\u043e\u0433\u0438\u0435 \u0437\u043d\u0430\u044e\u0442, \u0447\u0442\u043e \u0441\u0443\u0449\u0435\u0441\u0442\u0432\u0443\u044e\u0442 \u0440\u0430\u0437\u043b\u0438\u0447\u043d\u044b\u0435 \u0434\u0438\u0444\u0444\u0435\u0440\u0435\u043d\u0446\u0438\u0430\u043b\u044c\u043d\u044b\u0435 \u0443\u0440\u0430\u0432\u043d\u0435\u043d\u0438\u044f:\r\n\u043e\u0434\u043d\u043e\u0440\u043e\u0434\u043d\u044b\u0435, \u043d\u0435\u043e\u0434\u043d\u043e\u0440\u043e\u0434\u043d\u044b\u0435, \u0441 \u043f\u043e\u0441\u0442\u043e\u044f\u043d\u043d\u044b\u043c\u0438 \u043a\u043e\u044d\u0444\u0444\u0438\u0446\u0438\u0435\u043d\u0442\u0430\u043c\u0438 \u0438\u043b\u0438 \u0431\u0435\u0437 \u043d\u0438\u0445 \u0438\r\n\u0442.\u0434. \u0412 \u0434\u0430\u043d\u043d\u043e\u0439 \u0441\u0442\u0430\u0442\u044c\u0435 \u044f \u0445\u043e\u0447\u0443 \u0440\u0430\u0441\u0441\u043a\u0430\u0437\u0430\u0442\u044c \u0432\u0430\u043c \u043e\u0431 \u043e\u0434\u043d\u043e\u043c \u0432\u0438\u0434\u0435\r\n\u0434\u0438\u0444\u0444\u0435\u0440\u0435\u043d\u0446\u0438\u0430\u043b\u044c\u043d\u044b\u0445 \u0443\u0440\u0430\u0432\u043d\u0435\u043d\u0438\u0439 - \u0443\u0440\u0430\u0432\u043d\u0435\u043d\u0438\u0438 \u042d\u0439\u043b\u0435\u0440\u0430. \u041d\u0430\u0434\u0435\u044e\u0441\u044c, \u0447\u0442\u043e \u0434\u0430\u043d\u043d\u0430\u044f\r\n\u0441\u0442\u0430\u0442\u044c\u044f \u043f\u043e\u043c\u043e\u0436\u0435\u0442 \u0432\u0430\u043c \u0433\u043b\u0443\u0431\u0436\u0435 \u0440\u0430\u0437\u043e\u0431\u0440\u0430\u0442\u044c\u0441\u044f \u0432 \u0434\u0438\u0444\u0444\u0435\u0440\u0435\u043d\u0446\u0438\u0430\u043b\u044c\u043d\u044b\u0445 \u0443\u0440\u0430\u0432\u043d\u0435\u043d\u0438\u044f\u0445 \u0438\r\n\u043d\u0430\u0443\u0447\u0438\u0442\u044c\u0441\u044f \u0440\u0435\u0448\u0430\u0442\u044c \u043d\u043e\u0432\u044b\u0439 \u0438\u0445 \u0432\u0438\u0434.\r\n\r\n**\u041d\u0430\u0447\u043d\u0451\u043c. \u0414\u0438\u0444\u0444\u0435\u0440\u0435\u043d\u0446\u0438\u0430\u043b\u044c\u043d\u043e\u0435 \u0443\u0440\u0430\u0432\u043d\u0435\u043d\u0438\u0435 \u042d\u0439\u043b\u0435\u0440\u0430 \u0438\u043c\u0435\u0435\u0442 \u0441\u043b\u0435\u0434\u0443\u044e\u0449\u0438\u0439 \u0432\u0438\u0434:**\r\n\r\n$$\\\\boldsymbol{a_n x^n \\\\frac{d^n y}{dx^n} + a_{n-1} x^{n-1} \\\\frac{d^{n-1} y}{dx^{n-1}} + \\\\ldots + a_1 x \\\\frac{dy}{dx} + a_0 y = f(x)}$$\r\n\r\n\u0411\u043e\u043b\u0435\u0435 \u043e\u0431\u0449\u0438\u0439 \u0432\u0438\u0434 \u043c\u044b \u043c\u043e\u0436\u0435\u0442\u0435 \u043f\u043e\u0441\u043c\u043e\u0442\u0440\u0435\u0442\u044c \u0432 \u043a\u043e\u043d\u0446\u0435 \u0441\u0442\u0430\u0442\u044c\u0438\r\n\r\n\u041a\u0430\u043a \u0432\u044b \u043c\u043e\u0436\u0435\u0442\u0435 \u0437\u0430\u043c\u0435\u0442\u0438\u0442\u044c, \u0432\u0441\u0451 \u0434\u043e\u0432\u043e\u043b\u044c\u043d\u043e \u043f\u0440\u043e\u0441\u0442\u043e. \u0421\u0442\u0435\u043f\u0435\u043d\u044c \u0438\u043a\u0441\u0430 \u0441\u043e\u0432\u043f\u0430\u0434\u0430\u0435\u0442 \u0441\r\n\u043f\u043e\u0440\u044f\u0434\u043a\u043e\u043c \u043f\u0440\u043e\u0438\u0437\u0432\u043e\u0434\u043d\u043e\u0439 \u0438\u0433\u0440\u0435\u043a\u0430 \u043f\u043e \u0438\u043a\u0441\u0443.\r\n\r\n# II How to solve this?\r\n\r\n**\u0420\u0435\u0448\u0430\u0435\u0442\u0441\u044f \u0414\u0423 \u042d\u0439\u043b\u0435\u0440\u0430 \u043e\u0431\u044b\u0447\u043d\u043e\u0439 \u0437\u0430\u043c\u0435\u043d\u043e\u0439 \u0432\u0438\u0434\u0430:**\r\n\r\n$$\\\\boldsymbol{x=e^t}$$\r\n\r\n**\u0423 \u043d\u0430\u0441 \u043f\u043e\u044f\u0432\u043b\u044f\u0435\u0442\u0441\u044f \u043d\u043e\u0432\u0430\u044f \u0444\u0443\u043d\u043a\u0446\u0438\u044f $\\\\tilde{y}$ \u0437\u0430\u0432\u0438\u0441\u044f\u0449\u0430\u044f \u043e\u0442 t. \u0412\u044b\u0440\u0430\u0437\u0438\u043c\r\n\u043f\u0435\u0440\u0432\u0443\u044e \u0438 \u0432\u0442\u043e\u0440\u0443\u044e \u043f\u0440\u043e\u0438\u0437\u0432\u043e\u0434\u043d\u044b\u0435 \u0447\u0435\u0440\u0435\u0437 \u044d\u0442\u0443 \u0444\u0443\u043d\u043a\u0446\u0438\u044e:**\r\n\r\n$$\\\\begin{aligned}\r\n y\\'(x) &= \\\\frac{d(y(x))}{dx} = \\\\frac{dt}{dx} \\\\cdot \\\\frac{d}{dt}(\\\\tilde{y}\\')=e^{-t} \\\\cdot \\\\tilde{y}\\' \\\\\\\\\r\n y\\'\\'(x) &= \\\\frac{d(y\\'(x))}{dx} = \\\\frac{dt}{dx} \\\\cdot \\\\frac{d}{dt}(e^{-t} \\\\cdot \\\\tilde{y}\\')=e^{-2t} \\\\cdot (\\\\tilde{y}\\'\\' - \\\\tilde{y}\\')\r\n \\\\end{aligned}$$\r\n\r\n**\u0421 \u0431\u043e\u043b\u0435\u0435 \u0432\u044b\u0441\u043e\u043a\u0438\u043c\u0438 \u043f\u043e\u0440\u044f\u0434\u043a\u0430\u043c\u0438 \u0434\u0435\u043b\u0430\u0435\u043c \u0430\u043d\u0430\u043b\u043e\u0433\u0438\u0447\u043d\u043e.**\r\n\r\n**\u0422\u0435\u043f\u0435\u0440\u044c \u043f\u0440\u043e\u0438\u0437\u0432\u043e\u0434\u0438\u043c \u0437\u0430\u043c\u0435\u043d\u0443 \u0438\u043a\u0441\u043e\u0432, \u0438\u0433\u0440\u0435\u043a\u0430 \u0438 \u0435\u0433\u043e \u043f\u0440\u043e\u0438\u0437\u0432\u043e\u0434\u043d\u044b\u0445. \u0412 \u0438\u0442\u043e\u0433\u0435 \u043f\u043e\u043b\u0443\u0447\u0430\u0435\u043c \u0443\u0440\u0430\u0432\u043d\u0435\u043d\u0438\u0435 \u0441 \u043f\u043e\u0441\u0442\u043e\u044f\u043d\u043d\u044b\u043c\u0438 \u043a\u043e\u044d\u0444\u0444\u0438\u0446\u0435\u043d\u0442\u0430\u043c\u0438. \u0420\u0435\u0448\u0430\u044f \u0435\u0433\u043e \u0438 \u043d\u0430\u0445\u043e\u0434\u044f\r\n\u0437\u0430\u0432\u0438\u0441\u0438\u043c\u043e\u0441\u0442\u044c $\\\\tilde{y}(t)$ \u043c\u044b \u043f\u0440\u043e\u0438\u0437\u0432\u043e\u0434\u0438\u043c \u043e\u0431\u0440\u0430\u0442\u043d\u0443\u044e \u0437\u0430\u043c\u0435\u043d\u0443 t \u043d\u0430 x,\r\n\u0443\u0447\u0438\u0442\u044b\u0432\u0430\u044f \u0447\u0442\u043e $x=e^{t},t=\\\\ln x$.**\r\n\r\n\u0420\u0430\u0441\u0441\u043c\u043e\u0442\u0440\u0438\u043c \u043e\u0434\u0438\u043d \u043f\u0440\u0438\u043c\u0435\u0440 \u0440\u0435\u0448\u0435\u043d\u0438\u044f \u0414\u0423 \u042d\u0439\u043b\u0435\u0440\u0430.\r\n\r\n# III Example\r\n\r\n**\u0424\u0438\u043b\u0438\u043f\u043f\u043e\u0432 \u2116594**\r\n\r\n## \u0428\u0430\u0433 \u21161\r\n\r\n$$x^2 y\\'\\' + x y\\' + 4y = 10x.$$\r\n\r\n\u041f\u0440\u043e\u0438\u0437\u0432\u043e\u0434\u0438\u043c \u0437\u0430\u043c\u0435\u043d\u0443 \u0432\u0438\u0434\u0430 $x=e^t$ \u0438 \u043c\u0435\u043d\u044f\u044f \u0438\u0433\u0440\u0435\u043a\u0438 \u043d\u0430 $\\\\tilde{y}$,\r\n$\\\\tilde{y}\\'$, $\\\\tilde{y}\\'\\'$ :\r\n\r\n$$e^{2t} \\\\cdot e^{-2t}(\\\\tilde{y}\\'\\'-\\\\tilde{y}\\')+e^{t} \\\\cdot {e^{-t}}\\\\tilde{y}\\'+4\\\\tilde{y}=10e^{t}$$\r\n\r\n$$\\\\tilde{y}\\'\\'+\\\\tilde{y}\\'-\\\\tilde{y\\'}+4\\\\tilde{y}=10e^{t}$$\r\n\r\n\u041f\u043e\u043b\u0443\u0447\u0430\u0435\u043c \u0443\u0440\u0432\u043d\u0435\u043d\u0438\u0435 \u0441 \u043f\u043e\u0441\u0442\u043e\u044f\u043d\u043d\u044b\u043c\u0438 \u043a\u043e\u044d\u0444\u0444\u0438\u0446\u0435\u043d\u0442\u0430\u043c\u0438\r\n\r\n$$\\\\tilde{y}\\'\\' + 4\\\\tilde{y} = 10e^{t}$$\r\n\r\n## \u0428\u0430\u0433 \u21162\r\n\r\n\u0420\u0435\u0448\u0430\u0435\u043c \u043f\u043e\u043b\u0443\u0447\u0435\u043d\u043d\u043e\u0435 \u043d\u0435\u043e\u0434\u043e\u0440\u043e\u0434\u043d\u043e\u0435 \u0414\u0423\r\n\r\n$$\\\\lambda^2+4 = 0$$ $$\\\\lambda_{1,2} = \\\\pm 2i$$\r\n$$\\\\tilde{y_{0}}(t)=C_{1}\\\\cos2t+C_2\\\\sin2t$$ $$\\\\tilde{y_{p}}(t)=Ae^{t}$$\r\n$$\\\\tilde{y_{p}}\\'(t)=\\\\tilde{y_{p}}\\'\\'(t)=Ae^{t}$$\r\n\r\n\u041f\u043e\u0434\u0441\u0442\u0430\u0432\u043b\u044f\u0435\u043c \u0432 \u0443\u0440\u0430\u0432\u043d\u0435\u043d\u0438\u0435 (3) \u0438 \u043d\u0430\u0445\u043e\u0434\u0438\u043c A\r\n\r\n$$Ae^{t}+4Ae^{t}=10e^{t}$$ $$5Ae6{t}=10e^{t}\\\\Rightarrow A=2$$ \u0422\u043e\u0433\u0434\u0430\r\n\u043f\u043e\u043b\u0443\u0447\u0430\u0435\u043c,\u0447\u0442\u043e $$\\\\tilde{y_{p}}(t)=2e^{t}$$\r\n$$\\\\tilde{y}(t)=\\\\tilde{y_{0}}(t)+\\\\tilde{y_{p}}(t)=C_{1}\\\\cos 2t+C_{2}\\\\sin2t$$\r\n\r\n## \u0428\u0430\u0433 \u21163\r\n\r\n\u041e\u0431\u0440\u0430\u0442\u043d\u0430\u044f \u0437\u0430\u043c\u0435\u043d\u0430: $$x = e^{t} \\\\longrightarrow t = \\\\ln x$$\r\n$$\\\\boxed{y(x) = C_{1} \\\\cos(\\\\ln(x^2))+C_{2} \\\\sin(\\\\ln(x^{2}))+2x}$$\r\n\r\n# IV Remark\r\n\r\n\u0415\u0441\u043b\u0438 \u0432\u044b \u0432\u0441\u0442\u0440\u0435\u0447\u0430\u0435\u0442\u0435, \u043d\u0430\u043f\u0440\u0438\u043c\u0435\u0440, \u0442\u0430\u043a\u043e\u0435 \u0443\u0440\u0430\u0432\u043d\u0435\u043d\u0438\u0435:\r\n$$(2x - 1)^3 y\\'\\'\\'(x) + 4(2x - 1)^2 y\\'\\'(x) - 8(2x - 1) y\\'(x) = 32 \\\\ln(2x - 1)$$\r\n\r\n\u0422.\u0435. \u0432\u0438\u0434\u0430\r\n$$\\\\boldsymbol{\\\\sum_{k=0}^{n} a_k (\\\\alpha x + \\\\beta)^k y^{(k)}(x) = f(x)}$$\r\n\u0442\u043e \u0434\u0430\u043d\u043d\u043e\u0435 \u0443\u0440\u0430\u0432\u043d\u0435\u043d\u0438\u0435 \u044f\u0432\u043b\u044f\u0435\u0442\u0441\u044f **\u043e\u0431\u0449\u0438\u043c \u0432\u0438\u0434\u043e\u043c \u0414\u0423 \u042d\u0439\u043b\u0435\u0440\u0430 n-\u043f\u043e\u0440\u044f\u0434\u043a\u0430.**\r\n\r\n\u0418 \u0432 \u0434\u0430\u043d\u043d\u043e\u043c \u0441\u043b\u0443\u0447\u0430\u0435 \u043d\u0443\u0436\u043d\u043e \u0434\u0435\u043b\u0430\u0442\u044c \u0437\u0430\u043c\u0435\u043d\u0443 \u0432\u0438\u0434\u0430:\r\n$\\\\boldsymbol{\\\\alpha x+\\\\beta=e^{t}}$\r\n"}